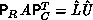, with 
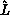unit lower-triangular, 
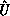upper-triangular, and permutation
matrices 
, 
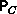, and solve Ax = b, using the
implicit pivoting approach described in [Skjellum:90d].
Sequentially, the triangular solves each require work proportional to
the number of entries in the respective triangular factor, including
fill-in. We have yet to find an example of sufficient size for which
we actually attain speedup for these operations, at least for the
sparse case. At most, we try to prevent these operations from becoming
competitive in cost to the B-mode factorization; we detail these
efforts in [Skjellum:90d]. In brief, the optimum grid shape for
the triangular solves has Q=1, and P somewhat reduced from what we
can use in all the other steps. As stated, P small seems better thus
far, although for many examples increasing the overhead as a function
of increasing P is not unacceptable (see [Skjellum:90d] and the
example below).