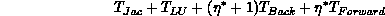Next: 9.5.6 Performance
Up: LU Factorization of
Previous: 9.5.4 New Data Distributions
Consider a fixed logical process grid of R processes, with 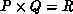 .
For the sake of argument, assume partial row pivoting during LU factorization
for the retention of numerical stability. Then, for the LU factorization, it
is well known that a scatter distribution is ``good'' for the matrix rows,
and optimal if no off-diagonal pivots were chosen. Furthermore, the
optimal column distribution is also scatter, because columns are chosen in
order for partial row pivoting. Compatibly, a scatter distribution of matrix
rows is also ``good'' for the triangular solves. However, for triangular
solves, the best column distribution is linear, because this implies less
intercolumn communication, as we detail below. In short, the optimal
configurations conflict, and because explicit redistribution is expensive, a
static compromise must be chosen. We address this need to compromise through
the one-parameter distribution function,
.
For the sake of argument, assume partial row pivoting during LU factorization
for the retention of numerical stability. Then, for the LU factorization, it
is well known that a scatter distribution is ``good'' for the matrix rows,
and optimal if no off-diagonal pivots were chosen. Furthermore, the
optimal column distribution is also scatter, because columns are chosen in
order for partial row pivoting. Compatibly, a scatter distribution of matrix
rows is also ``good'' for the triangular solves. However, for triangular
solves, the best column distribution is linear, because this implies less
intercolumn communication, as we detail below. In short, the optimal
configurations conflict, and because explicit redistribution is expensive, a
static compromise must be chosen. We address this need to compromise through
the one-parameter distribution function, 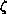 , described in the previous
section, offering a variable degree of scattering via the S-parameter. To
first order, changing S does not affect the cost of computing the Jacobian
(assuming columnwise finite-difference computation), because each process
column works independently.
, described in the previous
section, offering a variable degree of scattering via the S-parameter. To
first order, changing S does not affect the cost of computing the Jacobian
(assuming columnwise finite-difference computation), because each process
column works independently.
It's important to note that triangular solves derive no benefit from
Q > 1. The standard column-oriented solve keeps one process column active
at any given time. For any column distribution, the updated right-hand-side
vectors are retransmitted W times (process column-to-process column) during
the triangular solve-whenever the active process column changes. There are
at least 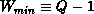 such transmissions (linear distribution), and
at most
such transmissions (linear distribution), and
at most 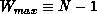 transmissions (scatter distribution). The
complexity of this retransmission is
transmissions (scatter distribution). The
complexity of this retransmission is 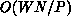 , representing quadratic work
in N for
, representing quadratic work
in N for 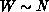 .
.
Calculation complexity for a sparse triangular solve is proportional to the
number of elements in the triangular matrix, with a low leading coefficient.
Often, there are 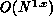 with x < 1 elements in the triangular
matrices, including fill. This operation is then
with x < 1 elements in the triangular
matrices, including fill. This operation is then 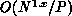 , which is
less than quadratic in N. Consequently, for large W, the retransmission
step is likely of greater cost than the original calculation. This
retransmission effect constrains the amount of scattering and size of Q in
order to have any chance of concurrent speedup in the triangular solves.
, which is
less than quadratic in N. Consequently, for large W, the retransmission
step is likely of greater cost than the original calculation. This
retransmission effect constrains the amount of scattering and size of Q in
order to have any chance of concurrent speedup in the triangular solves.
Using the one-parameter distribution with 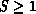 implies that
implies that
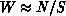 , so that the retransmission complexity is
, so that the retransmission complexity is 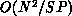 .
Consequently, we can bound the amount of retransmission work by making S
sufficiently large. Clearly,
.
Consequently, we can bound the amount of retransmission work by making S
sufficiently large. Clearly, 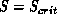 is a hard upper bound, because
we reach the linear distribution limit at that value of the parameter. We
suggest picking
is a hard upper bound, because
we reach the linear distribution limit at that value of the parameter. We
suggest picking 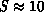 as a first guess, and
as a first guess, and 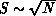 , more
optimistically. The former choice basically reduces retransmission effort by
an order of magnitude. Both examples in the following section illustrate the
effectiveness of choosing S by these heuristics.
, more
optimistically. The former choice basically reduces retransmission effort by
an order of magnitude. Both examples in the following section illustrate the
effectiveness of choosing S by these heuristics.
The two-parameter 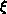 distribution can be used on the matrix rows to
trade off load balance in the factorizations and
triangular solves against the amount of (communication) effort needed
to compute the Jacobian. In particular, a greater degree of scattering
can dramatically increase the time required for a Jacobian computation
(depending heavily on the underlying equation structure and problem),
but significantly reduce load imbalance during the linear algebra
steps. The communication overhead caused by multiple process rows
suggests shifting toward smaller P and larger Q (a squatter grid),
in which case greater concurrency is attained in the Jacobian
computation, and the additional communication previously induced is
then somewhat mitigated. The one-parameter distribution used on the
matrix columns then proves effective in controlling the cost of the
triangular solves by choosing the minimally allowable amount of column
scattering.
distribution can be used on the matrix rows to
trade off load balance in the factorizations and
triangular solves against the amount of (communication) effort needed
to compute the Jacobian. In particular, a greater degree of scattering
can dramatically increase the time required for a Jacobian computation
(depending heavily on the underlying equation structure and problem),
but significantly reduce load imbalance during the linear algebra
steps. The communication overhead caused by multiple process rows
suggests shifting toward smaller P and larger Q (a squatter grid),
in which case greater concurrency is attained in the Jacobian
computation, and the additional communication previously induced is
then somewhat mitigated. The one-parameter distribution used on the
matrix columns then proves effective in controlling the cost of the
triangular solves by choosing the minimally allowable amount of column
scattering.
Let's specify make explicit the performance objectives we consider when tuning
S, and, more generally, when tuning the grid shape 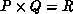 .
In the modified Newton iteration, for instance, a Jacobian
factorization is reused until convergence slows
unacceptably. An ``LU Factorization + Backsolve'' step is followed
by
.
In the modified Newton iteration, for instance, a Jacobian
factorization is reused until convergence slows
unacceptably. An ``LU Factorization + Backsolve'' step is followed
by 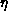 ``Forward + Backsolves,'' with
``Forward + Backsolves,'' with 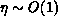 typically
(and varying dynamically throughout the calculation). Assuming an
averaged
typically
(and varying dynamically throughout the calculation). Assuming an
averaged 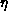 , say
, say 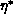 (perhaps as large as five
[Brenan:89a]), then our first-level performance goal is a
heuristic minimization of
(perhaps as large as five
[Brenan:89a]), then our first-level performance goal is a
heuristic minimization of
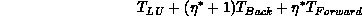
over S for fixed P, Q. 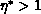 more heavily weights the reduction
of triangular solve costs versus B-mode factorization than we might at
first have assumed, placing a greater potential gain on the one-parameter
distribution for higher overall performance. We generally want heuristically
to optimize
more heavily weights the reduction
of triangular solve costs versus B-mode factorization than we might at
first have assumed, placing a greater potential gain on the one-parameter
distribution for higher overall performance. We generally want heuristically
to optimize
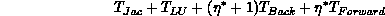
over S, P, Q, R. Then, the possibility of fine-tuning row and
column distributions is important, as is the use of non-power-of-two grid
shapes.





Next: 9.5.6 Performance
Up: LU Factorization of
Previous: 9.5.4 New Data Distributions
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
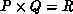 .
For the sake of argument, assume partial row pivoting during LU factorization
for the retention of numerical stability. Then, for the LU factorization, it
is well known that a scatter distribution is ``good'' for the matrix rows,
and optimal if no off-diagonal pivots were chosen. Furthermore, the
optimal column distribution is also scatter, because columns are chosen in
order for partial row pivoting. Compatibly, a scatter distribution of matrix
rows is also ``good'' for the triangular solves. However, for triangular
solves, the best column distribution is linear, because this implies less
intercolumn communication, as we detail below. In short, the optimal
configurations conflict, and because explicit redistribution is expensive, a
static compromise must be chosen. We address this need to compromise through
the one-parameter distribution function,
.
For the sake of argument, assume partial row pivoting during LU factorization
for the retention of numerical stability. Then, for the LU factorization, it
is well known that a scatter distribution is ``good'' for the matrix rows,
and optimal if no off-diagonal pivots were chosen. Furthermore, the
optimal column distribution is also scatter, because columns are chosen in
order for partial row pivoting. Compatibly, a scatter distribution of matrix
rows is also ``good'' for the triangular solves. However, for triangular
solves, the best column distribution is linear, because this implies less
intercolumn communication, as we detail below. In short, the optimal
configurations conflict, and because explicit redistribution is expensive, a
static compromise must be chosen. We address this need to compromise through
the one-parameter distribution function, 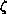 , described in the previous
section, offering a variable degree of scattering via the S-parameter. To
first order, changing S does not affect the cost of computing the Jacobian
(assuming columnwise finite-difference computation), because each process
column works independently.
, described in the previous
section, offering a variable degree of scattering via the S-parameter. To
first order, changing S does not affect the cost of computing the Jacobian
(assuming columnwise finite-difference computation), because each process
column works independently.





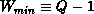 such transmissions (linear distribution), and
at most
such transmissions (linear distribution), and
at most 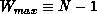 transmissions (scatter distribution). The
complexity of this retransmission is
transmissions (scatter distribution). The
complexity of this retransmission is 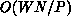 , representing quadratic work
in N for
, representing quadratic work
in N for 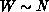 .
.
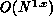 with x < 1 elements in the triangular
matrices, including fill. This operation is then
with x < 1 elements in the triangular
matrices, including fill. This operation is then 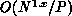 , which is
less than quadratic in N. Consequently, for large W, the retransmission
step is likely of greater cost than the original calculation. This
retransmission effect constrains the amount of scattering and size of Q in
order to have any chance of concurrent speedup in the triangular solves.
, which is
less than quadratic in N. Consequently, for large W, the retransmission
step is likely of greater cost than the original calculation. This
retransmission effect constrains the amount of scattering and size of Q in
order to have any chance of concurrent speedup in the triangular solves.
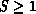 implies that
implies that
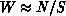 , so that the retransmission complexity is
, so that the retransmission complexity is 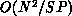 .
Consequently, we can bound the amount of retransmission work by making S
sufficiently large. Clearly,
.
Consequently, we can bound the amount of retransmission work by making S
sufficiently large. Clearly, 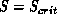 is a hard upper bound, because
we reach the linear distribution limit at that value of the parameter. We
suggest picking
is a hard upper bound, because
we reach the linear distribution limit at that value of the parameter. We
suggest picking 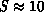 as a first guess, and
as a first guess, and 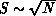 , more
optimistically. The former choice basically reduces retransmission effort by
an order of magnitude. Both examples in the following section illustrate the
effectiveness of choosing S by these heuristics.
, more
optimistically. The former choice basically reduces retransmission effort by
an order of magnitude. Both examples in the following section illustrate the
effectiveness of choosing S by these heuristics.
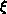 distribution can be used on the matrix rows to
trade off load balance
distribution can be used on the matrix rows to
trade off load balance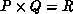 .
In the modified Newton iteration, for instance, a Jacobian
factorization is reused until convergence
.
In the modified Newton iteration, for instance, a Jacobian
factorization is reused until convergence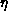 ``Forward + Backsolves,'' with
``Forward + Backsolves,'' with 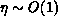 typically
(and varying dynamically throughout the calculation). Assuming an
averaged
typically
(and varying dynamically throughout the calculation). Assuming an
averaged 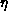 , say
, say 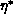 (perhaps as large as five
[
(perhaps as large as five
[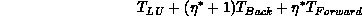
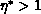 more heavily weights the reduction
of triangular solve costs versus B-mode factorization than we might at
first have assumed, placing a greater potential gain on the one-parameter
distribution for higher overall performance. We generally want heuristically
to optimize
more heavily weights the reduction
of triangular solve costs versus B-mode factorization than we might at
first have assumed, placing a greater potential gain on the one-parameter
distribution for higher overall performance. We generally want heuristically
to optimize