 tasks. Before delving into the details of the program,
let us first describe the algorithm at a high level.
tasks. Before delving into the details of the program,
let us first describe the algorithm at a high level.
In our next example we program a matrix-multiply algorithm described by Fox
et al. in [5]. The mmult program can be found at the end of this
section.
The mmult program will calculate C = AB, where
C, A, and B are all square matrices. For simplicity we
assume that m x m tasks will be used to calculate the solution.
Each task will calculate a subblock of the resulting matrix C. The
block size and the value of m is given as a command line argument to
the program. The matrices A and B are also stored as blocks distributed
over the  tasks. Before delving into the details of the program,
let us first describe the algorithm at a high level.
tasks. Before delving into the details of the program,
let us first describe the algorithm at a high level.
Assume we have a grid of m x m tasks. Each task (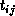 where
0 < = i,j < m) initially contains blocks
where
0 < = i,j < m) initially contains blocks 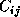 ,
, 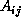 , and
, and
 . In the first step of the algorithm the tasks on the diagonal
(
. In the first step of the algorithm the tasks on the diagonal
(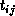 where i = j) send their block
where i = j) send their block 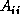 to all the other tasks
in row i. After the transmission of
to all the other tasks
in row i. After the transmission of 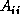 , all tasks calculate
, all tasks calculate
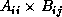 and add the result into
and add the result into 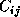 . In the next
step, the column blocks of B are rotated. That is,
. In the next
step, the column blocks of B are rotated. That is, 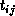 sends
its block of B to
sends
its block of B to 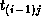 . (Task
. (Task 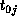 sends its B block
to
sends its B block
to 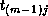 .) The tasks now return to the first step;
.) The tasks now return to the first step;
 is multicast to all other tasks in row i, and the
algorithm continues. After m iterations the C matrix contains A x B, and the B matrix has been rotated back into place.
is multicast to all other tasks in row i, and the
algorithm continues. After m iterations the C matrix contains A x B, and the B matrix has been rotated back into place.
Let's now go over the matrix multiply as it is programmed in PVM. In
PVM there is no restriction on which tasks may communicate with which
other tasks. However, for this program we would like to think of the
tasks as a two-dimensional conceptual torus. In order to enumerate the
tasks, each task joins the group mmult. Group ids are used to
map tasks to our torus. The first task to join a group is given the
group id of zero. In the mmult program, the task with group id zero
spawns the other tasks and sends the parameters for the matrix multiply
to those tasks. The parameters are m and bklsize: the square root of
the number of blocks and the size of a block, respectively. After all the
tasks have been spawned and the parameters transmitted,
pvm_barrier() is called to make sure all the tasks have joined
the group. If the barrier is not performed, later
calls to pvm_gettid() might fail since a task may not have yet
joined the group.
After the barrier, we store the task ids for the other tasks in our ``row'' in the array myrow. This is done by calculating the group ids for all the tasks in the row and asking PVM for the task id for the corresponding group id. Next we allocate the blocks for the matrices using malloc(). In an actual application program we would expect that the matrices would already be allocated. Next the program calculates the row and column of the block of C it will be computing. This is based on the value of the group id. The group ids range from 0 to m - 1 inclusive. Thus the integer division of (mygid/m) will give the task's row and (mygid mod m) will give the column, if we assume a row major mapping of group ids to tasks. Using a similar mapping, we calculate the group id of the task directly above and below in the torus and store their task ids in up and down, respectively.
Next the blocks are initialized by calling InitBlock(). This function simply initializes A to random values, B to the identity matrix, and C to zeros. This will allow us to verify the computation at the end of the program by checking that A = C.
Finally we enter the main loop to calculate the matrix multiply. First
the tasks on the diagonal multicast their block of A to the other tasks
in their row. Note that the array myrow actually contains the
task id of the task doing the multicast. Recall that pvm_mcast() will
send to all the tasks in the tasks array except the calling task. This
procedure works well in the case of mmult since we don't want to have to needlessly
handle the extra message coming into the multicasting task with an extra
pvm_recv(). Both the multicasting task and the tasks receiving the block
calculate the AB for the diagonal block and the block of B residing in
the task.
After the subblocks have been multiplied and added into the C block, we now shift the B blocks vertically. Specifically, we pack the block of B into a message, send it to the up task id, and then receive a new B block from the down task id.
Note that we use different message tags for sending the A blocks and the
B blocks as well as for different iterations of the loop. We also fully
specify the task ids when doing a pvm_recv(). It's tempting to use
wildcards for the fields of pvm_recv(); however, such a practice can be dangerous. For instance,
had we incorrectly calculated the value for up and used a wildcard
for the pvm_recv() instead of down,
we might have sent
messages to the wrong tasks without knowing it. In this example we fully
specify messages, thereby reducing the possibility of mistakes by receiving
a message from the wrong task or the wrong phase of the algorithm.
Once the computation is complete, we check to see that A = C, just to verify that the matrix multiply correctly calculated the values of C. This check would not be done in a matrix multiply library routine, for example.
It is not necessary to call pvm_lvgroup(), since PVM will
realize the task has exited and will remove it from the group. It is good
form, however, to leave the group before calling pvm_exit(). The
reset command from the PVM console will reset all the PVM groups. The
pvm_gstat command will print the status of any groups that
currently exist.