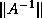
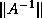
Bounds on the error 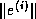 inevitably rely on bounds for
inevitably rely on bounds for 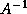 ,
since
,
since 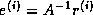 . There is a large number of problem dependent
ways to estimate
. There is a large number of problem dependent
ways to estimate 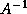 ; we mention a few here.
; we mention a few here.
When a splitting  is used to get an iteration
is used to get an iteration

then the matrix whose
inverse norm we need is 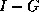 . Often, we know how to estimate
. Often, we know how to estimate
 if the splitting is a standard one such as Jacobi or SOR,
and the matrix
if the splitting is a standard one such as Jacobi or SOR,
and the matrix 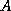 has special characteristics such as Property A.
Then we may estimate
has special characteristics such as Property A.
Then we may estimate 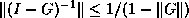 .
.
When 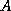 is symmetric positive definite, and Chebyshev acceleration with
adaptation of parameters is being used, then at each step the algorithm
estimates the largest and smallest eigenvalues
is symmetric positive definite, and Chebyshev acceleration with
adaptation of parameters is being used, then at each step the algorithm
estimates the largest and smallest eigenvalues 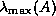 and
and
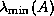 of
of 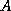 anyway.
Since
anyway.
Since 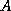 is symmetric positive definite,
is symmetric positive definite,
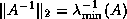 .
.
This adaptive estimation is often done using the Lanczos algorithm
(see section ![]() ),
which can usually provide good estimates of the
largest (rightmost) and smallest (leftmost) eigenvalues of a symmetric matrix
at the cost of a few matrix-vector multiplies.
For general nonsymmetric
),
which can usually provide good estimates of the
largest (rightmost) and smallest (leftmost) eigenvalues of a symmetric matrix
at the cost of a few matrix-vector multiplies.
For general nonsymmetric 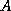 , we may apply
the Lanczos method to
, we may apply
the Lanczos method to 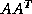 or
or 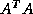 ,
and use the fact that
,
and use the fact that
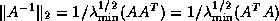 .
.
It is also possible to estimate 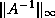 provided one is willing
to solve a few systems of linear equations with
provided one is willing
to solve a few systems of linear equations with 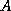 and
and 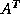 as coefficient
matrices. This is often done with dense linear system solvers, because the
extra cost of these systems is
as coefficient
matrices. This is often done with dense linear system solvers, because the
extra cost of these systems is 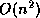 , which is small compared to the cost
, which is small compared to the cost
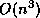 of the LU decomposition (see Hager [121],
Higham [124] and Anderson, et al. [3]).
This is not the case for iterative solvers, where the cost of these
solves may well be several times as much as the original linear system.
Still, if many linear systems with the same coefficient matrix and
differing right-hand-sides are to be solved, it is a viable method.
of the LU decomposition (see Hager [121],
Higham [124] and Anderson, et al. [3]).
This is not the case for iterative solvers, where the cost of these
solves may well be several times as much as the original linear system.
Still, if many linear systems with the same coefficient matrix and
differing right-hand-sides are to be solved, it is a viable method.
The approach in the last paragraph also lets us estimate the alternate
error bound 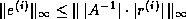 .
This may be much smaller than the simpler
.
This may be much smaller than the simpler
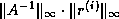 in the
case where the rows of
in the
case where the rows of 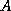 are badly scaled; consider the case of a
diagonal matrix
are badly scaled; consider the case of a
diagonal matrix 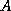 with widely varying diagonal entries. To
compute
with widely varying diagonal entries. To
compute 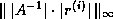 , let
, let 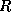 denote the diagonal
matrix with diagonal entries equal to the entries of
denote the diagonal
matrix with diagonal entries equal to the entries of 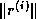 ; then
; then
 (see Arioli, Demmel and Duff [5]).
(see Arioli, Demmel and Duff [5]). 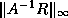 can be estimated using the
technique in the last paragraph since multiplying by
can be estimated using the
technique in the last paragraph since multiplying by
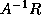 or
or 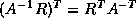 is no harder than multiplying
by
is no harder than multiplying
by 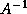 and
and 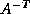 and also by
and also by  , a diagonal matrix.
, a diagonal matrix.