Survey of recent Krylov methods





Next: Preconditioners
Up: Iterative Methods
Previous: A short history
Research into the design of Krylov subspace methods for solving
nonsymmetric linear systems is an active field of research and new
methods are still emerging. In this book, we have included only the
best known and most popular methods, and in particular those for which
extensive computational experience has been gathered. In this
section, we shall briefly highlight some of the recent developments
and other methods not treated here. A survey of methods up to about
1991 can be found in Freund, Golub and
Nachtigal [106]. Two more recent reports by
Meier-Yang [151] and Tong [197] have extensive
numerical comparisons among various methods, including several more
recent ones that have not been discussed in detail in this book.
Several suggestions have been made to reduce the increase in memory
and computational costs in GMRES. An obvious one is to restart (this one is included
in § ): GMRES(
): GMRES(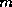 ). Another approach is to restrict
the GMRES search to a suitable subspace of some higher-dimensional
Krylov subspace. Methods based on this idea can be viewed as
preconditioned GMRES methods. The simplest ones exploit a fixed
polynomial preconditioner (see Johnson, Micchelli and
Paul [126],
Saad [183], and Nachtigal,
Reichel and Trefethen [159]).
In more sophisticated approaches, the
polynomial preconditioner is adapted to the iterations
(Saad [187]), or the preconditioner may even be some other
(iterative) method of choice (Van der Vorst and
Vuik [209], Axelsson and
Vassilevski [24]). Stagnation is prevented in the GMRESR
method (Van der Vorst and Vuik [209]) by including
LSQR steps in some phases of the process. In De Sturler and
Fokkema [64], part of the optimality of GMRES is
maintained in the hybrid method GCRO, in which the iterations of the
preconditioning method are kept orthogonal to the iterations of the
underlying GCR method. All these approaches have advantages for some
problems, but it is far from clear a priori which strategy is
preferable in any given case.
). Another approach is to restrict
the GMRES search to a suitable subspace of some higher-dimensional
Krylov subspace. Methods based on this idea can be viewed as
preconditioned GMRES methods. The simplest ones exploit a fixed
polynomial preconditioner (see Johnson, Micchelli and
Paul [126],
Saad [183], and Nachtigal,
Reichel and Trefethen [159]).
In more sophisticated approaches, the
polynomial preconditioner is adapted to the iterations
(Saad [187]), or the preconditioner may even be some other
(iterative) method of choice (Van der Vorst and
Vuik [209], Axelsson and
Vassilevski [24]). Stagnation is prevented in the GMRESR
method (Van der Vorst and Vuik [209]) by including
LSQR steps in some phases of the process. In De Sturler and
Fokkema [64], part of the optimality of GMRES is
maintained in the hybrid method GCRO, in which the iterations of the
preconditioning method are kept orthogonal to the iterations of the
underlying GCR method. All these approaches have advantages for some
problems, but it is far from clear a priori which strategy is
preferable in any given case.
Recent work has focused on endowing
the BiCG method with several desirable properties:
(1) avoiding breakdown;
(2) avoiding use of the transpose;
(3) efficient use of matrix-vector products;
(4) smooth convergence; and
(5) exploiting the work expended in forming the Krylov space with
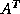 for further reduction of the residual.
for further reduction of the residual.
As discussed before, the BiCG method can have two kinds
of breakdown: Lanczos breakdown (the underlying Lanczos
process breaks down), and pivot breakdown (the
tridiagonal matrix 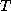 implicitly generated in the
underlying Lanczos process encounters a zero pivot when
Gaussian elimination without pivoting is used to factor it).
Although such exact breakdowns are very rare in practice, near
breakdowns can cause severe numerical stability problems.
implicitly generated in the
underlying Lanczos process encounters a zero pivot when
Gaussian elimination without pivoting is used to factor it).
Although such exact breakdowns are very rare in practice, near
breakdowns can cause severe numerical stability problems.
The pivot breakdown is the easier one to overcome and there have been
several approaches proposed in the literature. It should be noted
that for symmetric matrices, Lanczos breakdown cannot occur and the
only possible breakdown is pivot breakdown. The SYMMLQ and QMR
methods discussed in this book circumvent pivot breakdown by solving
least squares systems. Other methods tackling this problem can be
found
in Fletcher [98], Saad [181],
Gutknecht [113], and Bank and
Chan [29][28].
Lanczos breakdown is much more difficult to eliminate. Recently,
considerable attention has been given to analyzing the nature of the
Lanczos breakdown (see Parlett [172], and
Gutknecht [114][116]), as well as various look-ahead
techniques for remedying it (see Brezinski and
Sadok [39], Brezinski, Zaglia and
Sadok [41][40],
Freund and Nachtigal [102], Parlett [172],
Nachtigal [160], Freund, Gutknecht and
Nachtigal [101],
Joubert [129], Freund, Golub
and Nachtigal [106], and
Gutknecht [114][116]). However, the resulting
algorithms are usually too complicated to give in template form (some
codes of Freund and Nachtigal are available on netlib.)
Moreover, it is still not possible to eliminate breakdowns that
require look-ahead steps of arbitrary size (incurable breakdowns). So
far, these methods have not yet received much practical use but some
form of look-ahead may prove to be a crucial component in future
methods.
In the BiCG method, the need for matrix-vector multiplies with 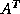 can be inconvenient as well as doubling the number of matrix-vector
multiplies compared with CG for each increase in the degree of the
underlying Krylov subspace.
Several recent methods have been proposed to overcome this drawback.
The most notable of these is the ingenious CGS method
by Sonneveld [192]
discussed earlier, which computes the square of the
BiCG polynomial without requiring
can be inconvenient as well as doubling the number of matrix-vector
multiplies compared with CG for each increase in the degree of the
underlying Krylov subspace.
Several recent methods have been proposed to overcome this drawback.
The most notable of these is the ingenious CGS method
by Sonneveld [192]
discussed earlier, which computes the square of the
BiCG polynomial without requiring 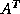 - thus obviating the need for
- thus obviating the need for 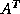 .
When BiCG converges, CGS is often an attractive,
faster converging alternative.
However, CGS also inherits (and often magnifies) the breakdown
conditions and the irregular convergence of
BiCG (see Van der Vorst [207]).
.
When BiCG converges, CGS is often an attractive,
faster converging alternative.
However, CGS also inherits (and often magnifies) the breakdown
conditions and the irregular convergence of
BiCG (see Van der Vorst [207]).
CGS also generated interest in the possibility of product
methods, which generate iterates corresponding to a product of the
BiCG polynomial with another polynomial of the same degree,
chosen to have certain desirable properties but
computable without recourse to 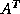 . The
Bi-CGSTAB method of Van der Vorst [207] is such an
example, in which the auxiliary polynomial is defined by a local
minimization chosen to smooth the convergence behavior.
Gutknecht [115] noted that Bi-CGSTAB could be viewed as a
product of BiCG and GMRES(1), and he suggested combining BiCG with
GMRES(2) for the even numbered iteration steps. This was anticipated
to lead to better convergence for the case where the eigenvalues of
. The
Bi-CGSTAB method of Van der Vorst [207] is such an
example, in which the auxiliary polynomial is defined by a local
minimization chosen to smooth the convergence behavior.
Gutknecht [115] noted that Bi-CGSTAB could be viewed as a
product of BiCG and GMRES(1), and he suggested combining BiCG with
GMRES(2) for the even numbered iteration steps. This was anticipated
to lead to better convergence for the case where the eigenvalues of
 are complex. A more efficient and more robust variant of this
approach has been suggested by Sleijpen and Fokkema
in [190], where they describe how to easily combine
BiCG with any GMRES(
are complex. A more efficient and more robust variant of this
approach has been suggested by Sleijpen and Fokkema
in [190], where they describe how to easily combine
BiCG with any GMRES(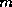 ), for modest
), for modest 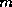 .
=-1
.
=-1
Many other basic methods can also be squared. For example, by
squaring the Lanczos procedure, Chan, de Pillis and
Van der Vorst [45] obtained
transpose-free implementations of BiCG and QMR. By squaring the QMR
method, Freund and Szeto [104] derived a transpose-free
QMR squared method which is quite competitive with CGS but with much
smoother convergence. Unfortunately, these methods
require an
extra matrix-vector product per step (three instead of two) which
makes them less efficient.
In addition to Bi-CGSTAB, several recent product methods have been
designed to smooth the convergence of CGS. One idea is to use the
quasi-minimal residual (QMR) principle to obtain smoothed iterates
from the Krylov subspace generated by other product methods.
Freund [105] proposed such a QMR version of CGS, which
he called TFQMR. Numerical experiments show that TFQMR in most
cases retains the desirable convergence features of CGS while
correcting its erratic behavior. The transpose free nature of TFQMR,
its low computational cost and its smooth convergence behavior make it
an attractive alternative to CGS. On the other hand, since the BiCG
polynomial is still used, TFQMR breaks down whenever CGS does. One
possible remedy would be to combine TFQMR with a look-ahead Lanczos
technique but this appears to be quite complicated and no methods of
this kind have yet appeared in the literature. Recently, Chan et. al. [46] derived a similar QMR version of
Van der Vorst's Bi-CGSTAB method, which is called QMRCGSTAB. These
methods offer smoother convergence over CGS and Bi-CGSTAB with little
additional cost.
There is no clear best Krylov subspace method at this time, and there
will never be a best overall Krylov subspace method. Each of
the methods is a winner in a specific problem class, and the main
problem is to identify these classes and to construct new methods for
uncovered classes. The paper by Nachtigal, Reddy and
Trefethen [158] shows that for any of a group of
methods (CG, BiCG, GMRES, CGNE, and CGS), there is a class of problems
for which a given method is the winner and another one is the loser.
This shows clearly that there will be no ultimate method. The best we
can hope for is some expert system that guides the user in his/her
choice. Hence, iterative methods will never reach the robustness of
direct methods, nor will they beat direct methods for all problems.
For some problems, iterative schemes will be most attractive,
and for others, direct methods (or
multigrid). We hope to find suitable methods
(and preconditioners) for classes of very large problems that we are
yet unable to solve by any known method, because of CPU-restrictions,
memory, convergence problems, ill-conditioning, et cetera.





Next: Preconditioners
Up: Iterative Methods
Previous: A short history
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
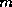 ). Another approach is to restrict
the GMRES search to a suitable subspace of some higher-dimensional
Krylov subspace. Methods based on this idea can be viewed as
preconditioned GMRES methods. The simplest ones exploit a fixed
polynomial preconditioner (see Johnson, Micchelli and
Paul [126],
Saad [183], and Nachtigal,
Reichel and Trefethen [159]).
In more sophisticated approaches, the
polynomial preconditioner is adapted to the iterations
(Saad [187]), or the preconditioner may even be some other
(iterative) method of choice (Van der Vorst and
Vuik [209], Axelsson and
Vassilevski [24]). Stagnation is prevented in the GMRESR
method (Van der Vorst and Vuik [209]) by including
LSQR steps in some phases of the process. In De Sturler and
Fokkema [64], part of the optimality of GMRES is
maintained in the hybrid method GCRO, in which the iterations of the
preconditioning method are kept orthogonal to the iterations of the
underlying GCR method. All these approaches have advantages for some
problems, but it is far from clear a priori which strategy is
preferable in any given case.
). Another approach is to restrict
the GMRES search to a suitable subspace of some higher-dimensional
Krylov subspace. Methods based on this idea can be viewed as
preconditioned GMRES methods. The simplest ones exploit a fixed
polynomial preconditioner (see Johnson, Micchelli and
Paul [126],
Saad [183], and Nachtigal,
Reichel and Trefethen [159]).
In more sophisticated approaches, the
polynomial preconditioner is adapted to the iterations
(Saad [187]), or the preconditioner may even be some other
(iterative) method of choice (Van der Vorst and
Vuik [209], Axelsson and
Vassilevski [24]). Stagnation is prevented in the GMRESR
method (Van der Vorst and Vuik [209]) by including
LSQR steps in some phases of the process. In De Sturler and
Fokkema [64], part of the optimality of GMRES is
maintained in the hybrid method GCRO, in which the iterations of the
preconditioning method are kept orthogonal to the iterations of the
underlying GCR method. All these approaches have advantages for some
problems, but it is far from clear a priori which strategy is
preferable in any given case.
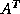 for further reduction of the residual.
for further reduction of the residual.
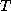 implicitly generated in the
underlying Lanczos process encounters a zero pivot when
Gaussian elimination without pivoting is used to factor it).
Although such exact breakdowns are very rare in practice, near
breakdowns can cause severe numerical stability problems.
implicitly generated in the
underlying Lanczos process encounters a zero pivot when
Gaussian elimination without pivoting is used to factor it).
Although such exact breakdowns are very rare in practice, near
breakdowns can cause severe numerical stability problems.
 are complex. A more efficient and more robust variant of this
approach has been suggested by Sleijpen and Fokkema
in
are complex. A more efficient and more robust variant of this
approach has been suggested by Sleijpen and Fokkema
in