

If 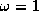 , the SOR method simplifies
to the Gauss-Seidel method. A theorem due to
Kahan [130] shows that SOR fails to
converge if
, the SOR method simplifies
to the Gauss-Seidel method. A theorem due to
Kahan [130] shows that SOR fails to
converge if  is outside the interval
is outside the interval  . Though
technically the term underrelaxation
should be used when
. Though
technically the term underrelaxation
should be used when 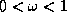 , for convenience the term
overrelaxation is now used for any value
of
, for convenience the term
overrelaxation is now used for any value
of 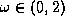 .
.
In general, it is not possible to compute in advance the value
of  that is optimal with respect to the rate of convergence of
SOR. Even when it is possible to compute the optimal value
for
that is optimal with respect to the rate of convergence of
SOR. Even when it is possible to compute the optimal value
for  , the expense of such computation is usually prohibitive.
Frequently, some heuristic estimate is used, such as
, the expense of such computation is usually prohibitive.
Frequently, some heuristic estimate is used, such as 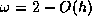 where
where  is the mesh spacing of the discretization of the
underlying physical domain.
is the mesh spacing of the discretization of the
underlying physical domain.
If the coefficient matrix 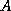 is symmetric and positive definite, the
SOR iteration is guaranteed to converge for any
value of
is symmetric and positive definite, the
SOR iteration is guaranteed to converge for any
value of  between 0 and 2, though the choice of
between 0 and 2, though the choice of  can
significantly affect the rate at which the SOR iteration
converges. Sophisticated implementations of the SOR
algorithm (such as that found in ITPACK [140]) employ adaptive
parameter estimation schemes to try to home in on the appropriate
value of
can
significantly affect the rate at which the SOR iteration
converges. Sophisticated implementations of the SOR
algorithm (such as that found in ITPACK [140]) employ adaptive
parameter estimation schemes to try to home in on the appropriate
value of  by estimating the rate at which the iteration is
converging.
by estimating the rate at which the iteration is
converging.
Adaptive methods: Iterative methods that collect information
about the coefficient matrix during the iteration process, and use
this to speed up convergence.
Symmetric matrix: See: Matrix properties.
Diagonally dominant matrix: See: Matrix properties
 -Matrix: See: Matrix properties.
Positive definite matrix: See: Matrix properties.
Matrix properties: We call a square matrix
-Matrix: See: Matrix properties.
Positive definite matrix: See: Matrix properties.
Matrix properties: We call a square matrix 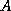
 for all
for all  ,
, 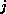 .
.
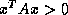 for all nonzero vectors
for all nonzero vectors  .
.
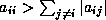 .
.
 -matrix
-matrix
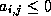 for
for 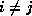 , and it
is nonsingular with
, and it
is nonsingular with  for all
for all 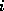 ,
, 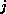 .
.
For coefficient matrices of a special class called consistently
ordered with property A (see
Young [217]), which includes certain orderings of matrices
arising from the discretization of elliptic PDEs, there is a direct
relationship between the spectra of the Jacobi
and SOR iteration matrices. In principle, given the
spectral radius 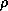 of the
Jacobi iteration matrix, one can determine a priori the theoretically optimal value of
of the
Jacobi iteration matrix, one can determine a priori the theoretically optimal value of  for SOR:
for SOR:
This is seldom done, since calculating the spectral radius of the
Jacobi matrix requires an impractical amount of computation. However,
relatively inexpensive rough estimates of 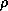 (for example, from
the power method, see Golub and Van Loan [p. 351]GoVL:matcomp)
can yield reasonable estimates for the optimal value of
(for example, from
the power method, see Golub and Van Loan [p. 351]GoVL:matcomp)
can yield reasonable estimates for the optimal value of  .
.