




Next: Singular Value Decomposition (SVD)
Up: Standard Eigenvalue and Singular
Previous: Symmetric Eigenproblems (SEP)
Contents
Index
The nonsymmetric eigenvalue problem is to find the eigenvalues, 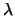 ,
and corresponding eigenvectors,
,
and corresponding eigenvectors, 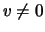 , such that
, such that
A real matrix  may have complex eigenvalues, occurring as complex conjugate
pairs. More precisely, the vector
may have complex eigenvalues, occurring as complex conjugate
pairs. More precisely, the vector 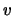 is called a right
eigenvector of
is called a right
eigenvector of  , and a vector
, and a vector 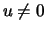 satisfying
satisfying
is called a left eigenvector of  .
.
This problem can be solved
via the Schur factorization of  ,
defined in the real case as
,
defined in the real case as
where 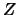 is an orthogonal matrix and
is an orthogonal matrix and 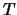 is an upper quasi-triangular matrix
with
is an upper quasi-triangular matrix
with 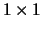 and
and 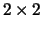 diagonal blocks,
the
diagonal blocks,
the 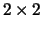 blocks
corresponding to complex conjugate pairs
of eigenvalues of
blocks
corresponding to complex conjugate pairs
of eigenvalues of  . In the
complex case the Schur factorization is
. In the
complex case the Schur factorization is
where 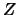 is unitary and
is unitary and 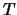 is a complex upper triangular matrix.
is a complex upper triangular matrix.
The columns of 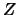 are called the Schur vectors.
For each
are called the Schur vectors.
For each 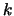
 , the first
, the first 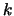 columns of
columns of 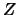 form an orthonormal
basis for the invariant subspace corresponding to the
first
form an orthonormal
basis for the invariant subspace corresponding to the
first 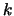 eigenvalues on the diagonal of
eigenvalues on the diagonal of 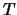 . Because this
basis is orthonormal, it is preferable in many
applications to compute Schur vectors rather than
eigenvectors. It is possible to order the Schur
factorization so that any desired set of
. Because this
basis is orthonormal, it is preferable in many
applications to compute Schur vectors rather than
eigenvectors. It is possible to order the Schur
factorization so that any desired set of 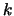 eigenvalues
occupy the
eigenvalues
occupy the 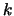 leading positions on the diagonal of
leading positions on the diagonal of 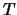 .
.
Two pairs of drivers are provided, one pair focusing on the Schur
factorization, and the other pair on the eigenvalues and eigenvectors
as shown in Table 2.5:
- LA_GEES: a simple driver that computes all or
part of the Schur factorization of
 , with optional ordering of the
eigenvalues;
, with optional ordering of the
eigenvalues;
- LA_GEESX: an expert driver that can additionally
compute condition numbers for the average of a selected subset of the
eigenvalues, and for the corresponding right invariant subspace;
- LA_GEEV: a simple driver that computes all the
eigenvalues of
 , and (optionally) the right or left eigenvectors (or both);
, and (optionally) the right or left eigenvectors (or both);
- LA_GEEVX: an expert driver that can additionally
balance the matrix to improve the conditioning of the eigenvalues and
eigenvectors, and compute condition numbers for the eigenvalues or right
eigenvectors (or both).





Next: Singular Value Decomposition (SVD)
Up: Standard Eigenvalue and Singular
Previous: Symmetric Eigenproblems (SEP)
Contents
Index
Susan Blackford
2001-08-19
![]() ,
and corresponding eigenvectors,
,
and corresponding eigenvectors, ![]() , such that
, such that