




Next: Arguments
Up: Standard Nonsymmetric Eigenvalue Problems
Previous: LA_GEESX
Contents
Index
LA_GEESX computes for a real/complex square matrix  , the
eigenvalues, the real-Schur/complex-Schur form
, the
eigenvalues, the real-Schur/complex-Schur form 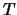 , and, optionally, the
matrix of Schur vectors
, and, optionally, the
matrix of Schur vectors 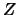 , where
, where 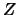 is orthogonal/unitary.
This gives the Schur factorization
is orthogonal/unitary.
This gives the Schur factorization
Optionally, it also orders the eigenvalues on the diagonal of the
Schur form so that selected eigenvalues are at the top left,
computes a reciprocal condition number for the average of the
selected eigenvalues, and computes a reciprocal condition
number for the right invariant subspace corresponding to the
selected eigenvalues. The leading columns of 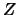 form an
orthonormal basis for this invariant subspace.
form an
orthonormal basis for this invariant subspace.
A real matrix is in real-Schur form if it is block upper triangular with
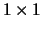 and
and 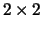 blocks along the main diagonal.
blocks along the main diagonal.
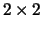 blocks are standardized in the form
blocks are standardized in the form
where 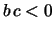 . The eigenvalues of such a block are
. The eigenvalues of such a block are
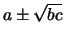 .
.
A complex matrix is in complex-Schur form if it is upper triangular.





Next: Arguments
Up: Standard Nonsymmetric Eigenvalue Problems
Previous: LA_GEESX
Contents
Index
Susan Blackford
2001-08-19
![]() , the
eigenvalues, the real-Schur/complex-Schur form
, the
eigenvalues, the real-Schur/complex-Schur form ![]() , and, optionally, the
matrix of Schur vectors
, and, optionally, the
matrix of Schur vectors ![]() , where
, where ![]() is orthogonal/unitary.
This gives the Schur factorization
is orthogonal/unitary.
This gives the Schur factorization
![\begin{displaymath}\left[ \begin{array}{cc} a & b \\ c & a \end{array} \right] \end{displaymath}](img706.gif)