




Next: Arguments
Up: Generalized Linear Least Squares
Previous: LA_GGGLM
Contents
Index
LA_GGGLM solves the general (Gauss-Markov) linear model (GLM) problem:
where  and
and  are real or complex rectangular matrices and
are real or complex rectangular matrices and  is a real or
complex vector.
Further,
is a real or
complex vector.
Further,  is
is 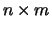 ,
,  is
is 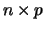 , and
, and  is
is 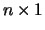 , and
it is assumed that
, and
it is assumed that
These conditions ensure that the GLM problem has unique solution
vectors 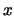 and
and 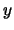 . The problem is solved using the generalized
. The problem is solved using the generalized 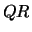 factorization
of
factorization
of  and
and  .
.
If matrix  is square and nonsingular, then the
GLM problem is equivalent to the weighted linear least squares problem
is square and nonsingular, then the
GLM problem is equivalent to the weighted linear least squares problem
Susan Blackford
2001-08-19