




Next: Arguments
Up: Generalized Linear Least Squares
Previous: LA_GGLSE
Contents
Index
LA_GGLSE solves the linear equality-constrained least squares
(LSE) problem:
where  and
and  are real or complex rectangular matrices and
are real or complex rectangular matrices and 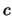 and
and
 are real or complex vectors. Further,
are real or complex vectors. Further,  is
is 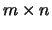 ,
,  is
is
 ,
, 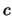 is
is  and
and  is
is 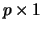 , and it is
assumed that
, and it is
assumed that
These conditions ensure that the 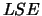 problem has a unique solution
problem has a unique solution 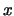 .
This is obtained using the generalized
.
This is obtained using the generalized 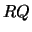 factorization of the matrices
factorization of the matrices
 and
and  .
.
Susan Blackford
2001-08-19
