




Next: Example (from Program LA_GELSS_EXAMPLE)
Up: Linear Least Squares Problems
Previous: Purpose
Contents
Index
- A
- (input/output) REAL or COMPLEX
array, shape
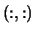 .
.
On entry, the matrix  .
.
On exit, the first 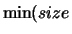 (A,1),
(A,1), 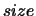 (A,2))
rows of
(A,2))
rows of  are overwritten with its right singular vectors, stored rowwise.
are overwritten with its right singular vectors, stored rowwise.
- B
- (input/output) REAL or COMPLEX
array, shape
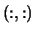 with
with 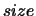 (B,1)
(B,1) 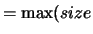 (A,1),
(A,1),
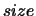 (A,2)) or shape
(A,2)) or shape 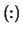 with
with 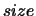 (B)
(B)
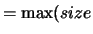 (A,1),
(A,1), 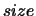 (A,2)).
(A,2)).
On entry, the matrix  .
.
On exit, the solution matrix 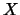 .
.
If 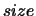 (A,1)
(A,1) 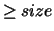 (A,2) and RANK
(A,2) and RANK
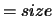 (A,2), the residual
sum-of-squares for the solution in a column of B is given
by the sum of squares of elements in rows
(A,2), the residual
sum-of-squares for the solution in a column of B is given
by the sum of squares of elements in rows
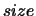 (A,2)
(A,2)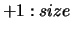 (A,1) of that column.
(A,1) of that column.
- RANK
- Optional (output) INTEGER.
The effective rank of  , i.e., the number of singular values
of
, i.e., the number of singular values
of  which are greater than the product
which are greater than the product
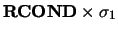 ,
where
,
where 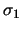 is the greatest singular value.
is the greatest singular value.
- S
- Optional (output) REAL array,
shape
 with
with 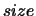 (S)
(S) 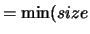 (A,1),
(A,1),
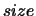 (A,2)).
(A,2)).
The singular values of  in decreasing order.
in decreasing order.
The condition number of  in the 2-norm is
in the 2-norm is
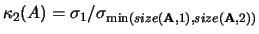 .
.
- RCOND
- Optional (input) REAL.
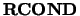 is used to determine the effective rank of
is used to determine the effective rank of  .
.
Singular values
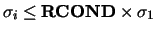 are treated
as zero.
are treated
as zero.
Default value:
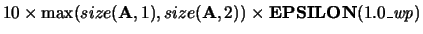 , where wp is the working precision.
, where wp is the working precision.
- INFO
- Optional (output) INTEGER.
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INFO}...
...ments of an intermediate
bidiagonal form did not converge to zero.
\end{infoarg}](img568.gif)
If 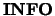 is not present and an error occurs, then the program is
terminated with an error message.
is not present and an error occurs, then the program is
terminated with an error message.
References: [1] and [17,9,20].





Next: Example (from Program LA_GELSS_EXAMPLE)
Up: Linear Least Squares Problems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INFO}...
...ments of an intermediate
bidiagonal form did not converge to zero.
\end{infoarg}](img568.gif)
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INFO}...
...ments of an intermediate
bidiagonal form did not converge to zero.
\end{infoarg}](img568.gif)