




Next: Arguments
Up: Symmetric/Hermitian Positive Definite Linear
Previous: Purpose
Contents
Index
-
24.
- If FACT = 'N', the matrix
 is factored as
is factored as
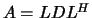 , where
, where 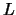 is a unit lower bidiagonal matrix and
is a unit lower bidiagonal matrix and 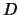 is a diagonal matrix. The
factorization can also be regarded as having the form
is a diagonal matrix. The
factorization can also be regarded as having the form
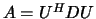 , where
, where 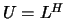 .
.
-
25.
- If the leading minor of order
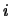 of
of  is not positive definite,
then the routine returns with
is not positive definite,
then the routine returns with
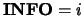 . Otherwise, the factored
form of
. Otherwise, the factored
form of  is used to estimate the condition number of
is used to estimate the condition number of
 . If the reciprocal of the condition number is less than machine
precision,
. If the reciprocal of the condition number is less than machine
precision,
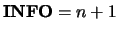 , where
, where 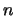 is the order of
is the order of  , is returned as a warning.
However, the routine still goes on to solve for
, is returned as a warning.
However, the routine still goes on to solve for 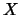 . Iterative refinement
is applied to improve the computed solution.
. Iterative refinement
is applied to improve the computed solution.
-
26.
- LA_PTSVX also optionally computes, for each solution vector
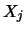 ,
the estimated forward error bound and the componentwise relative backward error.
,
the estimated forward error bound and the componentwise relative backward error.
Susan Blackford
2001-08-19