Further Details: Error Bounds for the Generalized Singular Value Decomposition





Next: Error Bounds for
Up: Error Bounds for
Previous: Error Bounds for
The GSVD algorithm used in LAPACK ([12][10][62])
is backward stable:
Let the computed GSVD of A and B be 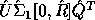 and
and
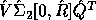 .
This is nearly the exact GSVD of
A + E and B + F in the following sense. E and F are small:
.
This is nearly the exact GSVD of
A + E and B + F in the following sense. E and F are small: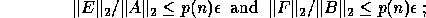
there exist small
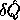 ,
, 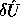 , and
, and 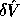 such that
such that
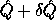 ,
,
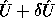 , and
, and
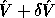 are exactly orthogonal (or unitary):
are exactly orthogonal (or unitary):
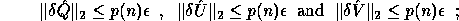
and
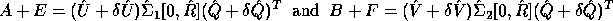
is the exact GSVD of A + E and B + F. Here p(n) is a modestly growing function of n, and
we take p(n) = 1 in the above code fragment.
Let  and
and 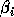 be the square roots of the diagonal entries of the exact
be the square roots of the diagonal entries of the exact
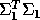 and
and 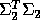 ,
and let
,
and let 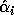 and
and 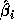 the square roots of the diagonal entries
of the computed
the square roots of the diagonal entries
of the computed 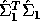 and
and 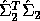 .
Let
.
Let
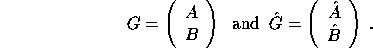
Then provided G and 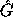 have full rank n, one can show [61][74] that
have full rank n, one can show [61][74] that
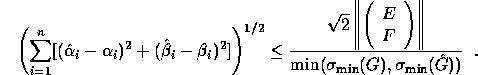
In the code fragment we approximate the numerator of the last expression by
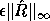 and approximate the denominator by
and approximate the denominator by
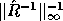 in order to compute SERRBD;
STRCON returns an approximation RCOND to
in order to compute SERRBD;
STRCON returns an approximation RCOND to
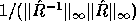 .
.
We assume that the rank r of G equals n, because otherwise the
 s and
s and 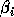 s are not well determined. For example, if
s are not well determined. For example, if
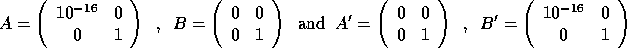
then A and B have
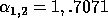 and
and 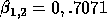 , whereas
, whereas
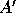 and
and 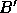 have
have
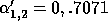 and
and 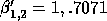 , which
are completely different, even though
, which
are completely different, even though 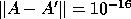 and
and
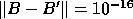 . In this case,
. In this case, 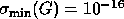 ,
so G is nearly rank-deficient.
,
so G is nearly rank-deficient.
The reason the code fragment assumes m > = n is that in this case 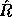 is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If m < = n, then the
first m rows of
is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If m < = n, then the
first m rows of 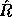 are
stored in A, and the last m - n rows of
are
stored in A, and the last m - n rows of 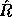 are stored in B. This
complicates the computation of RCOND: either
are stored in B. This
complicates the computation of RCOND: either 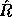 must be copied to
a single array before calling STRCON, or else the lower level subroutine SLACON
must be used with code capable of solving linear equations with
must be copied to
a single array before calling STRCON, or else the lower level subroutine SLACON
must be used with code capable of solving linear equations with 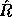 and
and 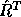 as coefficient matrices.
as coefficient matrices.





Next: Error Bounds for
Up: Error Bounds for
Previous: Error Bounds for
Tue Nov 29 14:03:33 EST 1994
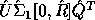 and
and
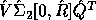 .
This is nearly the exact GSVD of
A + E and B + F in the following sense. E and F are small:
.
This is nearly the exact GSVD of
A + E and B + F in the following sense. E and F are small: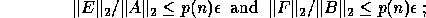
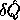 ,
, 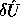 , and
, and 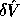 such that
such that
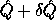 ,
,
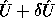 , and
, and
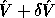 are exactly orthogonal (or unitary):
are exactly orthogonal (or unitary):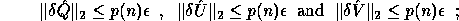
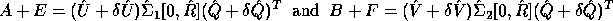
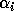 and
and 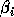 be the square roots of the diagonal entries of the exact
be the square roots of the diagonal entries of the exact
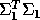 and
and 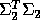 ,
and let
,
and let 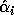 and
and 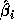 the square roots of the diagonal entries
of the computed
the square roots of the diagonal entries
of the computed 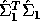 and
and 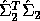 .
Let
.
Let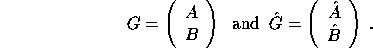
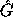 have full rank n, one can show [61][74] that
have full rank n, one can show [61][74] that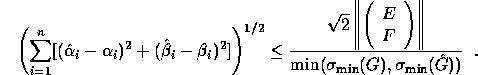
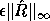 and approximate the denominator by
and approximate the denominator by
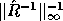 in order to compute SERRBD;
STRCON returns an approximation RCOND to
in order to compute SERRBD;
STRCON returns an approximation RCOND to
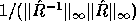 .
.
 s and
s and 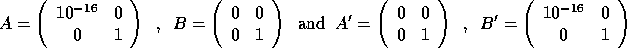
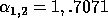 and
and 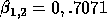 , whereas
, whereas
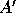 and
and 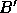 have
have
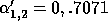 and
and 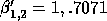 , which
are completely different, even though
, which
are completely different, even though 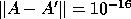 and
and
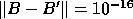 . In this case,
. In this case, 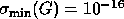 ,
so G is nearly rank-deficient.
,
so G is nearly rank-deficient.
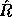 is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If m < = n, then the
first m rows of
is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If m < = n, then the
first m rows of 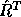 as coefficient matrices.
as coefficient matrices.