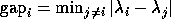 is
the absolute gap
between
is
the absolute gap
between 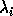 and the nearest other eigenvalue.
and the nearest other eigenvalue.
The error analysis of the driver routine xSYGV, or xHEGV in the complex case
(see subsection 2.2.5.1),
goes as follows.
In all cases
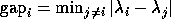 is
the absolute gap
between
is
the absolute gap
between 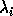 and the nearest other eigenvalue.
and the nearest other eigenvalue.
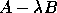 .
The computed eigenvalues
.
The computed eigenvalues 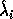 can differ
from true eigenvalues
can differ
from true eigenvalues 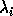 by at most about
by at most about
The angular difference between the computed eigenvector
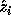 and a true eigenvector
and a true eigenvector 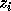 is
is
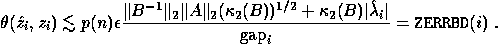
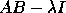 or
or 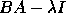 .
The computed eigenvalues
.
The computed eigenvalues 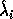 can differ
from true eigenvalues
can differ
from true eigenvalues 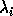 by at most about
by at most about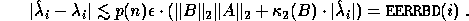
The angular difference between the computed eigenvector
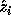 and a true eigenvector
and a true eigenvector 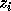 is
is
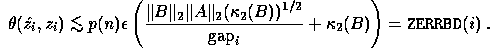
The code fragments above replace p(n) by 1, and makes sure neither RCONDB nor RCONDZ is so small as to cause overflow when used as divisors in the expressions for error bounds.
These error bounds are large when B is ill-conditioned with respect to
inversion (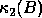 is large). It is often the case that the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention three ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude
is large). It is often the case that the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention three ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude![]() :
:
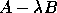 . Let
. Let 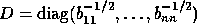 be a diagonal matrix.
Then replace B by DBD and A by DAD in the above bounds.
be a diagonal matrix.
Then replace B by DBD and A by DAD in the above bounds.
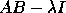 or
or 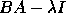 .
Let
.
Let 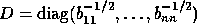 be a diagonal matrix.
Then replace B by DBD and A by
be a diagonal matrix.
Then replace B by DBD and A by 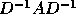 in the above bounds.
in the above bounds.
The second way to get tighter bounds does not actually supply guaranteed
bounds, but its estimates are often better in practice.
It is not guaranteed because it assumes the algorithm is backward stable,
which is not necessarily true when B is ill-conditioned.
It estimates the chordal distance between a
true eigenvalue 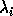 and a computed eigenvalue
and a computed eigenvalue 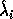 :
:
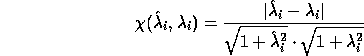
To interpret this measure we write 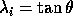 and
and 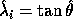 . Then
. Then
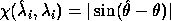 .
In other words, if
.
In other words, if 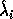 represents the one-dimensional subspace
represents the one-dimensional subspace
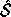 consisting of the line through the origin with slope
consisting of the line through the origin with slope 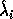 ,
and
,
and 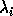 represents the analogous subspace S, then
represents the analogous subspace S, then
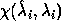 is the sine of the acute angle
is the sine of the acute angle 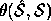 between these
subspaces.
Thus X is bounded by one, and is small when both arguments are
large
between these
subspaces.
Thus X is bounded by one, and is small when both arguments are
large![]() .
It applies only to the first problem,
.
It applies only to the first problem, 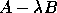 :
:
Suppose a computed eigenvalueof
is the exact eigenvalue of a perturbed problem
. Let
be the unit eigenvector (
) for the exact eigenvalue
. Then if ||E|| is small compared to |A|, and if ||F|| is small compared to ||B||, we have
The third way applies only to the first problem 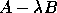 , and only
when A is positive definite. We use a different algorithm:
, and only
when A is positive definite. We use a different algorithm:
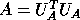 , using xPOTRF.
, using xPOTRF.
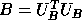 , using xPOTRF.
, using xPOTRF.
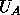 ,
, 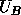 using xTGSJA. The squares of the generalized singular
values are the desired eigenvalues.
using xTGSJA. The squares of the generalized singular
values are the desired eigenvalues.
Other yet more refined algorithms and error bounds are discussed in [78][73][13], and will be available in future releases.