Error Bounds for the Singular Value Decomposition





Next: Further Details: Error
Up: Accuracy and Stability
Previous: Computing and
The singular value decomposition (SVD) of a
real m-by-n matrix A is defined as follows. Let r = min(m , n).
The the SVD of A is 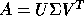 (
(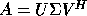 in the complex case),
where
U and V are orthogonal (unitary) matrices and
in the complex case),
where
U and V are orthogonal (unitary) matrices and
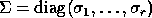 is diagonal,
with
is diagonal,
with 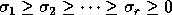 .
The
.
The 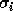 are the singular values of A and the leading
r columns
are the singular values of A and the leading
r columns 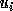 of U and
of U and 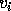 of V the
left and right singular vectors, respectively.
The SVD of a general matrix is computed by xGESVD
(see subsection 2.2.4).
of V the
left and right singular vectors, respectively.
The SVD of a general matrix is computed by xGESVD
(see subsection 2.2.4).
The approximate error
bounds
for the computed singular values
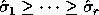 are
are

The approximate error bounds for the computed singular vectors
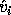 and
and 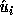 ,
which bound the acute angles between the computed singular vectors and true
singular vectors
,
which bound the acute angles between the computed singular vectors and true
singular vectors 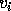 and
and 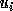 , are
, are

These bounds can be computing by the following code fragment.
EPSMCH = SLAMCH( 'E' )
* Compute singular value decomposition of A
* The singular values are returned in S
* The left singular vectors are returned in U
* The transposed right singular vectors are returned in VT
CALL SGESVD( 'S', 'S', M, N, A, LDA, S, U, LDU, VT, LDVT,
$ WORK, LWORK, INFO )
IF( INFO.GT.0 ) THEN
PRINT *,'SGESVD did not converge'
ELSE IF ( MIN(M,N) .GT. 0 ) THEN
SERRBD = EPSMCH * S(1)
* Compute reciprocal condition numbers for singular
* vectors
CALL SDISNA( 'Left', M, N, S, RCONDU, INFO )
CALL SDISNA( 'Right', M, N, S, RCONDV, INFO )
DO 10 I = 1, MIN(M,N)
VERRBD( I ) = EPSMCH*( S(1)/RCONDV( I ) )
UERRBD( I ) = EPSMCH*( S(1)/RCONDU( I ) )
10 CONTINUE
END IF
For example,
if
 and
and

then the singular values, approximate error bounds, and true errors are given below.

Tue Nov 29 14:03:33 EST 1994
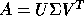 (
(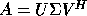 in the complex case),
where
U and V are orthogonal (unitary) matrices and
in the complex case),
where
U and V are orthogonal (unitary) matrices and
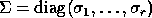 is diagonal,
with
is diagonal,
with 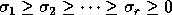 .
The
.
The 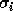 are the singular values of A and the leading
r columns
are the singular values of A and the leading
r columns 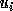 of U and
of U and 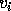 of V the
left and right singular vectors, respectively.
The SVD of a general matrix is computed by xGESVD
(see subsection 2.2.4).
of V the
left and right singular vectors, respectively.
The SVD of a general matrix is computed by xGESVD
(see subsection 2.2.4).
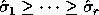 are
are
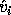 and
and 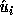 ,
which bound the acute angles between the computed singular vectors and true
singular vectors
,
which bound the acute angles between the computed singular vectors and true
singular vectors 
 and
and
