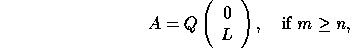
The QL and RQ factorizations are given by
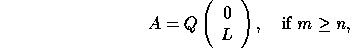
and
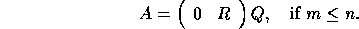
These factorizations are computed by xGEQLF and xGERQF, respectively; they are less commonly used than either the QR or LQ factorizations described above, but have applications in, for example, the computation of generalized QR factorizations [2].
All the factorization routines discussed here (except xTZRQF) allow arbitrary m and n, so that in some cases the matrices R or L are trapezoidal rather than triangular. A routine that performs pivoting is provided only for the QR factorization.
---------------------------------------------------------------------------
Type of
factorization Single precision Double precision
and matrix Operation real complex real complex
---------------------------------------------------------------------------
QR, general factorize with pivoting SGEQPF CGEQPF DGEQPF ZGEQPF
factorize, no pivoting SGEQRF CGEQRF DGEQRF ZGEQRF
generate Q SORGQR CUNGQR DORGQR ZUNGQR
multiply matrix by Q SORMQR CUNMQR DORMQR ZUNMQR
---------------------------------------------------------------------------
LQ, general factorize, no pivoting SGELQF CGELQF DGELQF ZGELQF
generate Q SORGLQ CUNGLQ DORGLQ ZUNGLQ
multiply matrix by Q SORMLQ CUNMLQ DORMLQ ZUNMLQ
---------------------------------------------------------------------------
QL, general factorize, no pivoting SGEQLF CGEQLF DGEQLF ZGEQLF
generate Q SORGQL CUNGQL DORGQL ZUNGQL
multiply matrix by Q SORMQL CUNMQL DORMQL ZUNMQL
---------------------------------------------------------------------------
RQ, general factorize, no pivoting SGERQF CGERQF DGERQF ZGERQF
generate Q SORGRQ CUNGRQ DORGRQ ZUNGRQ
multiply matrix by Q SORMRQ CUNMRQ DORMRQ ZUNMRQ
---------------------------------------------------------------------------
RQ, trapezoidal factorize, no pivoting STZRQF CTZRQF DTZRQF ZTZRQF
---------------------------------------------------------------------------
Table 2.9: Computational routines for orthogonal factorizations