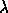 and corresponding
eigenvectors
and corresponding
eigenvectors
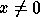 such that
such that
Given two square matrices A and B,
the generalized nonsymmetric eigenvalue problem is to find
the eigenvalues 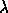 and corresponding
eigenvectors
and corresponding
eigenvectors
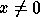 such that
such that

or
find the eigenvalues 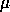 and corresponding eigenvectors
and corresponding eigenvectors
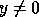 such that
such that

Note that these problems are equivalent with  and
and  if neither
if neither 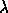 nor
nor 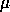 is zero.
In order to deal with the case that
is zero.
In order to deal with the case that 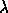 or
or 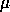 is zero, or nearly so,
the LAPACK routines return two values,
is zero, or nearly so,
the LAPACK routines return two values,  and
and 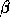 , for each
eigenvalue, such that
, for each
eigenvalue, such that 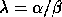 and
and  .
.
More precisely,  and
and 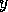 are called right eigenvectors. Vectors
are called right eigenvectors. Vectors
 or
or 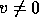 satisfying
satisfying

If the determinant of 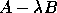 is zero for all values of
is zero for all values of 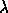 ,
the eigenvalue problem is called singular, and is signaled by some
,
the eigenvalue problem is called singular, and is signaled by some
 (in the presence of roundoff,
(in the presence of roundoff, 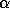 and
and 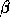 may
be very small). In this case the eigenvalue problem is very ill-conditioned,
and in fact some of the other nonzero values of
may
be very small). In this case the eigenvalue problem is very ill-conditioned,
and in fact some of the other nonzero values of  and
and 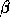 may be
indeterminate [21][80][71].
may be
indeterminate [21][80][71].
The generalized nonsymmetric eigenvalue problem can be solved via the generalized Schur factorization of the pair A,B, defined in the real case as
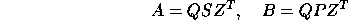
where Q and Z are orthogonal matrices, P is upper triangular, and S is an upper quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks, the 2-by-2 blocks corresponding to complex conjugate pairs of eigenvalues of A,B. In the complex case the Schur factorization is
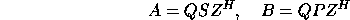
where Q and Z are unitary and S and P are both upper triangular.
The columns of Q and Z are called generalized Schur vectors and span pairs of deflating subspaces of A and B [72]. Deflating subspaces are a generalization of invariant subspaces: For each k (1 < = k < = n), the first k columns of Z span a right deflating subspace mapped by both A and B into a left deflating subspace spanned by the first k columns of Q.
Two simple drivers are provided for the nonsymmetric problem
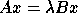 :
:
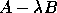 ;
;