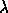 , and corresponding eigenvectors ,
, and corresponding eigenvectors , 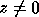 , such that
, such that
The symmetric eigenvalue problem is to find the eigenvalues ,
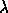 , and corresponding eigenvectors ,
, and corresponding eigenvectors , 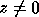 , such that
, such that
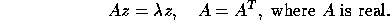
For the Hermitian eigenvalue problem we have
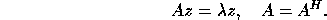
For both problems the eigenvalues 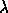 are real.
are real.
When all eigenvalues and eigenvectors have been computed, we write:

where 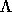 is a diagonal matrix whose diagonal elements are the
eigenvalues , and Z is an orthogonal (or unitary) matrix whose columns
are the eigenvectors. This is the classical spectral factorization
of A.
is a diagonal matrix whose diagonal elements are the
eigenvalues , and Z is an orthogonal (or unitary) matrix whose columns
are the eigenvectors. This is the classical spectral factorization
of A.
Three types of driver routines are provided for symmetric or Hermitian eigenproblems:
Different driver routines are provided to take advantage of special structure or storage of the matrix A, as shown in Table 2.5.
In the future LAPACK will include routines based on the Jacobi algorithm [76][69][24], which are slower than the above routines but can be significantly more accurate.