Many communication packages can be classified as having operations based on one dimensional arrays, which are the machine representation for linear algebra's vector class. In programming linear algebra problems, however, it is more natural to express all operations in terms of matrices. Vectors and scalars are, of course, simply subclasses of matrices. On computers, a linear algebra matrix is represented by a two dimensional array (2D array), and therefore the BLACS operate on 2D arrays.
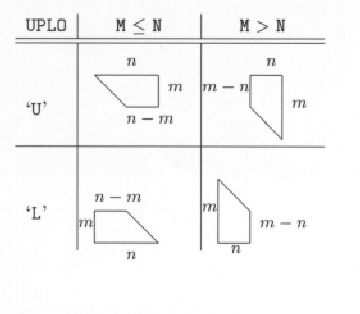
The BLACS recognize the two most common classes of matrices for dense linear algebra. The first of these classes consist of general rectangular matrices, which in machine storage are 2D arrays consisting of M rows and N columns, with a leading dimension, LDA, that determines the distance between successive columns in memory.
The general rectangular matrices therefore take the following parameters as input when determining what array to operate on:

The packing of arrays (if required) so that they may be sent efficiently
is hidden, allowing the user to concentrate on the logical matrix,
rather than how the data is organized in the machine's memory.