



Next: 8 Summary
Up: No Title
Previous: 6 Performance Modelling
The estimated runtime is represented in Figures 4 and
5. The 2D partitioning allows us to study a variety of 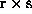 process structures. The part of the computational work is gridded
and the Hippis part is dashed. Since we assume a series-parallel
model, there is no overlap between these parts. The intra-system
communication is of course existing and is considered. But this part takes less
than 1% and cannot be seen in the figures.
process structures. The part of the computational work is gridded
and the Hippis part is dashed. Since we assume a series-parallel
model, there is no overlap between these parts. The intra-system
communication is of course existing and is considered. But this part takes less
than 1% and cannot be seen in the figures.
The computational work is always split into a small gridded and
a largely gridded part. Here the ideal minimum runtime on a single C90
system (i.e. sequential_runtime/16) is standardised to be 1. This part is
represented by the small gridded bar. The influence of different partitionings
as provided by the IFS is only marginal in the case of this large problem. In
the case of 2 and 4 systems per cluster, we see nearly 1/2 or even 1/4 for
the estimated runtime. Here the ideal runtime is of course
sequential_runtime/32 or sequential_runtime/64 respectively. In all
cases the overall runtime is dominated by the part called ideal runtime in our
large example.
The remaining amount of computational work (largely gridded part)
is caused mainly by more inefficient vectorisation and load imbalancing in the
parallel case. We considered only those examples where load imbalancing is of
minor importance. Load imbalancing would occur for an 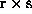 process
structure, if s is not a good divisor of the number of levels z. In
this case, load imbalancing would occur at least within the Fourier space (cf.
Figure 1 and [5]).
process
structure, if s is not a good divisor of the number of levels z. In
this case, load imbalancing would occur at least within the Fourier space (cf.
Figure 1 and [5]).
The Hippi time cost are split into a densely dashed part for start-up time
and a sparsely dashed part for transmission time. The start-up time does not
play any role for large problems. Therefore, the best
partitioning is here 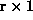 . For the
. For the 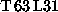 -case, however, start-up
time takes a considerable amount of time in particular on a 4-system cluster
and with high values of r. Since the vectorisation is more efficient with
high r-values, the best partitioning is here a squared partitioning.
-case, however, start-up
time takes a considerable amount of time in particular on a 4-system cluster
and with high values of r. Since the vectorisation is more efficient with
high r-values, the best partitioning is here a squared partitioning.
Figure 3 shows better efficiency on a 4-system cluster than on
a 2-system cluster for our largest example. To explain this effect, we remind
that a 4-system cluster has 6 Hippi channels and a 2-system cluster has only
one. This is of importance in cases showing high transmission time via
Hippi.
We considered also other mappings (cf. [5]) but the column
mapping used here showed the best results as long as 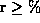 .
.




Next: 8 Summary
Up: No Title
Previous: 6 Performance Modelling
top500@rz.uni-mannheim.de
Tue May 28 14:38:25 PST 1996
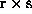 process structures. The part of the computational work is gridded
and the Hippis part is dashed. Since we assume a series-parallel
model, there is no overlap between these parts. The intra-system
communication is of course existing and is considered. But this part takes less
than 1% and cannot be seen in the figures.
process structures. The part of the computational work is gridded
and the Hippis part is dashed. Since we assume a series-parallel
model, there is no overlap between these parts. The intra-system
communication is of course existing and is considered. But this part takes less
than 1% and cannot be seen in the figures.
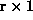 . For the
. For the 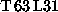 -case, however, start-up
time takes a considerable amount of time in particular on a 4-system cluster
and with high values of r. Since the vectorisation is more efficient with
high r-values, the best partitioning is here a squared partitioning.
-case, however, start-up
time takes a considerable amount of time in particular on a 4-system cluster
and with high values of r. Since the vectorisation is more efficient with
high r-values, the best partitioning is here a squared partitioning.
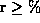 .
.